TREAP
The Treap
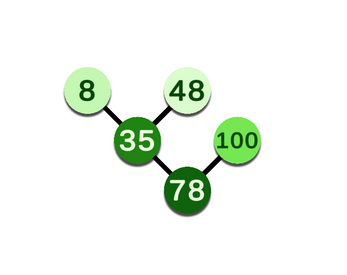
The Treap, a portmanteau of "tree" and "heap", is a unique type of binary search tree, a linked set of ordered keys that follows three simple rules:
- Every right branch has a value greater than its parent.
- Every left branch has a value less than its parent.
- Every branch is lighter in color than its parent (has higher "priority").
Huh?
I would recommend hitting the random button a few times and seeing what happens! You will quickly begin to notice some patterns in how the tree tries to balance itself to follow the three rules. If you’re interested in more technical details, read on.
This data structure is used in computer science as a way to store large amounts of data with quick access. Suppose you have a huge alphabetically ordered database of customer names, and you want to retrieve the data attached to one of the customers. If they were stored in a list, the computer would have to potentially iterate through every single one of them before it finds a match. Binary trees quicken the search process, by instead storing each entry as one of up to 2 branches off previous entries, one that is greater alphabetically and the other that is less. To find the right entry, the computer now just travels up the tree, taking a right or left if the search query is alphabetically greater or less than the current node. With this model, the computer only has to travel as deep as the height of the tree. As it turns out, the number of accesses approaches just log(n) for most implementations, where n is the number of elements in the tree, instead of having to potentially iterate through all n elements.
So what do the colors mean?
What I just described is only the theory behind how a regular binary tree functions, but this is a treap, not a tree!
There is a problem with regular binary trees. Suppose that you enter all of your customer names into the tree in alphabetical order. Each subsequent entry will get tacked on as a right branch, and you will just end up with a giant list. Regular binary trees work well when all the entries are added in a random order but suffer from lopsided-ness otherwise.
To fix that, we assign each node a random color (officially a “priority”) between 0 and 1 and maintain that parent nodes must be darker in color (lower priority) than their children. When a node is added to the tree, we travel through the tree branching left and right until we find an empty spot where it can fit as a leaf. Then, if the node is darker than its parent, the tree makes “rotations” to shuffle it further down the tree until it is in a spot where the third rule is enforced. These rotations are the magic of the treap, as they maintain the first two rules of the treap while correcting for the third. In the end, the tree becomes probabilistically balanced for large numbers of entries, so we can still have very quick log(n) accesses.
What is this for?
I made this as a visualization tool for anyone interested in or studying computer science. There is not much out there that really lets you “see” how binary trees work, and I personally believe that visualizations like these can really help make some of these concepts much more intuitive. In the future, I hope to extend these animations to other types of data structures.
| Status | Released |
| Platforms | HTML5 |
| Author | Magus Studios |
| Genre | Educational |
| Made with | Unity |
| Tags | Visualization |
Leave a comment
Log in with itch.io to leave a comment.